Leslie Texas
By Leslie A. Texas
In her article, “What is the Mathematics Design Collaborative?” in last month’s newsletter, Renee’ Yates introduced the Mathematics Design Collaborative and described a framework and shared tools. This article builds upon that introduction and focuses specifically on the power of the “C” in MDC.
The Mathematics Design Collaborative (MDC) is just as it suggests, a collaborative of people involved in the work of improving mathematics teaching and learning. It is not a program or curriculum, but rather a group of people using various principles, strategies and tools to assess the effectiveness of what is being taught and what is being learned.
This “assessment for learning” process is one of the shared principles of MDC. Marnie Thompson and Dylan Wiliam in their whitepaper, “Tight But Loose: A Conceptual Framework for Scaling Up School Reform,” introduce the Big Idea of Assessment for Learning as, “students and teachers, using evidence of learning to adapt teaching and learning, to meet immediate learning needs, minute-to-minute and day-by-day.”
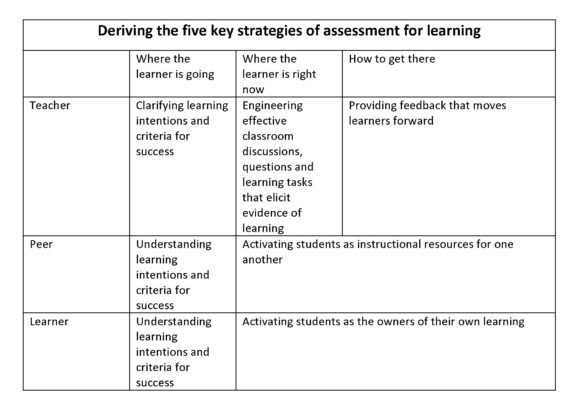
Thompson and Wiliam also identify five key strategies of assessment for learning:
- Clarifying and sharing learning intentions and criteria for success
- Engineering effective discussions, questions and tasks that elicit evidence of learning.
- Providing feedback that moves learners forward.
- Activating students as the owners of their own learning.
- Activating students as instructional resources for one another.
These strategies are the focus of MDC and provide a structure for teachers as they design and plan for effective instruction. Effective instruction must engage students in the depth of the standard by including opportunities to develop conceptual understanding, procedural fluency and application. In addition, teachers need to explicitly plan opportunities for students to build the mathematical practices necessary to be successful.
In order to support teachers in this instructional process, a common set of tools from The Mathematics Assessment Project are utilized. These include both formative and summative assessments that reveal students’ deeper understanding of mathematical concepts as well as their ability to apply that knowledge to non-routine problems.
One of those tools is the Classroom Challenges – also known as Formative Assessment Lessons (FALs) – which are used to assess students’ understanding of concepts and their ability to utilize mathematical practices in a various situations. The lessons are designed to engage students, both individually and with others, in ways that uncover misconceptions but provide opportunities for students to learn and move to the next level of understanding. This information is great feedback for teachers to reflect on the effectiveness of previous instruction, as well as make adjustments to future instruction.
One of the biggest misconceptions of MDC is that it is all about the Formative Assessment Lessons. This could not be further from the truth. The FALs are a primary tool in the beginning because they prompt a conversation around what is needed to move mathematics teaching and learning forward.
First, these assessments, if implemented with fidelity, expose the fact that instruction does not always align with the depth of the standards and what is required of students to demonstrate proficiency. This is particularly true if students have only been taught procedurally. Students often struggle in the FALs because they are asked to engage in the content in very nontraditional ways and they are not able to apply what they know in the new context.
Second, the lessons place an emphasis on the students’ ability to utilize the mathematical practices. If these are not developed through daily instruction, students will struggle during the lesson. By experiencing the lessons and understanding the students’ struggles, teachers gain a better understanding of what effective instruction needs to include.
In addition to prompting conversation, the FALs are used as models of how to incorporate the five strategies of assessment for learning. Detailed lesson plans with identified student misconceptions, possible feedback questions and other facilitation notes help teachers understand how to develop their own lessons for meeting the expectations of the standards.
This is why the collaborative in MDC is the most significant piece. It is in professional learning communities – school, district, state, cooperatives – where people can engage in the work, understand the purpose and evolve that the true power of MDC exists. MDC is not about the tools; it is the people.
MDC goes beyond placing Formative Assessment Lessons into curriculum maps and implementing the lessons once a unit. It is an ongoing analysis of mathematics teaching and learning and the collaborative conversations prompting shifts in instruction to meet the needs of the learner.
One organization taking part in the collaborative is the Southern Regional Education Board. To learn more about their involvement in MDC, go here.
Leslie A. Texas is a national consultant and author of “Strategies for Common Core Mathematics: Implementing the Standards for Mathematical Practice K-5, 6-8, 9-12” and “Strategic Journeys for Building Logical Reasoning: Activities Across the Content Areas K-5, 6-8, 9-12.”
Leave A Comment